GEOMETRIA TETRAEDRULUI

Profesor Mariana Ganea,

                                                                                                        Şcoala Generală nr.12, Tg.Jiu

„Azi facem matematica ce va fi folosită mâine şi mai ales poimâine. Că dacă n-am face-o azi, poimâine ar trebui s-o importăm.” Grigore Moisil

 

Voi reda mai jos un mod unitar principalele proprietati dintr-un tetraedru fiind structurata pe trei capitole.

CAP. I realizeaza un studiu sistematic al celei mai simple configuraţii spaţiale – tetraedrul. Pentru a permite aprofundarea teoriei si spre a edifica tehnici geometrice cu caracter de generalitate, au fost alese probleme care exprima idei generale in evolu­ţia contemporana a geometriei. Impartirea pe paragrafe: definiţii, notatii, tetraedre par­ticulare, volum, drepte concurente, plane concurente, puncte coplanare, reiaţii metrice, inegalitati geometrice, maxime si minime, expresii constante, elemente fixe si, respec­tiv, secţiuni urmăreşte ordinea fireasca a noţiunilor, teoremelor si metodelor acestei discipline.

Am acordat o atentie deosebita identificării unor tipuri de probleme, le-am zice „mai speciale precum si a unor metode de rezolvare a acestora. Fara a crede in „retete” consider ca, in marea diversitate a problemelor de geometrie, o anumita „tipiza­re” poate sa devină fructuoasa.Multe dintre problemele alese, prin gradul mare de generalitate pe care il au, con­stituie o adevarata completare a teoriei.

In paragrafele 6 si 7 sunt prezentate generalizări in spaţiul tridimensional ale teoremei lui Menelaus, relaţiilor: van Aubel, Stewart.

Paragrafele 8, 9, 10, 11 sunt consacrate problemelor care sunt cel mai greu de abordat cand dorim sa pătrundem in tainele tetraedrului: inegalitati, maxime si minime, expresii constante, elemente fixe.

In paragraful 12 este prezentat un algoritm pentru determinarea unei secţiuni in tetraedru cat si formule referitoare la secţiuni.

CAP. al ll-lea cuprinde principalele proprietati ale tetraedrelor ortocentrice, echifaciale, tridreptunghice, izodinamice (izofaciale) si respectiv regulate; de asemenea corelaţia plan – spaţiu este punctata de analogia triunghi – tetraedru.

In fine, CAP. al III-lea apare ca o justificare a paragrafelor 8, 9, 10. 11 din CAP. I; am putea spune ca un răspuns la întrebarea: De ce geometria tetraedrului?

Intrucât bibliografia in acest domeniu este deosebit de vasta, am intampinat unele dificuitati in sistematizarea materialului.

 

CAPITOLUL I – PROPRIETATI FUNDAMENTALE

§ 1. DEFINIŢII, NOTATII

Figura din spaţiu cu proprietati asemanatoare cu cele ale triunghiului este tetraedrul. Denumirea tetraedrului provine de la cuvintele greceşti tetra=patru, hedra=fata.

Definiţie: Daca punctele A,B,C,D, nu sunt coplanare, mulţimea ABCD = [ABC] U [ABD] U [ACD] U [BCD] se numeşte tetraedru. Punctele A,B,C,D, sunt vârfurile, segmentele închise AB,AC,AD,BD,CD, sunt muchiile, iar suprafeţele triunghiulare [ABC], [ABD], [ACD], [BCD] sunt suprafeţele tetraedrului.

Observaţie: Pentru desenarea tetraedrului, prin convenţie, consideram ca fetele sunt placi semitransparente si atunci unele muchii, presupuse in spatele unor fete, se traseaza cu linii intrerupte. interiorul tetraedrului ABCD, se noteaza cu Int. (ABCD) si este intersectia semispatiilor deschise determinate de planele fetelor si vârful opus respectiv, interiorul tetrae­drului este o mulţime convexa, fiind o intersectie de mulţimi convexe.

Pentru tetraedrul ABCD se vor utiliza frecvent urmatoarele notatii:

-lungimile muchiilor: BC = a, CA = b, AB = c, AD = l, BD = m, CD = n.

-aria fetei [ABC] se va nota SABC sau, mai concis, S; pentru a uşura alinierea unor formule vom folosi si notatia |ABC|.

-planul (BCD), adica „fata opusa” lui D se noteaza Df.

-unghiurile diedre: ^ C(AB)D va fi renotat ^AB, etc.

-unghiuri triedre; ^A(BCD) se va nota când nu vor fi posibile confuzii cu Â, etc,

-alte notatii consacrate se vor evidenţia pe parcurs. In general pentru centre de greutate se va folosi majuscula G (convenabil indexata), pentru ortocentre majuscula H, pentru lungimi de inaltimi litera h, pentru sfere circumscrise simboluri ¤(O, R).

§ 2. TETRAEDRE PARTICULARE

Trecerea de la triunghi la tetraedru marcheaza si un remarcabil salt al particulari­zărilor posibile, din punct de vedere numeric, al interesului special si al interferenţelor intre criteriile de particularizare. Cele mai importante tipuri de tetraedre particulare vor fi studiate separat in capitolul al II-lea.

1.Punând condiţii asupra fetelor tetraedrului se remarca:

-tetraedrul izofacial sau piramida triunghiulara regulata: o fata triunghi echilateral, cele­lalte trei isoscele.

-tetraedrul echifacial: avand fetele triunghiuri echivalente, sau, ceea ce revine la acelaşi lucru, de perimetre egale.

-tetraedrul regulat: toate fetele sunt triunghiuri echilaterale.

-tetraedre tridreptunghice: avand trei fete triunghiuri dreptunghice, cu unghiuri drepte in acelaşi varf, etc.

Prin condiţii asupra lungimilor muchiilor se disting tetraedrele:

-echifaciaie (muchii opuse egale);

regulate;

-izodinamice (produsele muchiilor opuse egale);

-„Crelle” (sumele muchiilor opuse egale);

-ortocentrice (sumele patratelor muchiilor opuse egale), etc.

Exista si alte criterii de particularizare:

-dupa unghiuri diedre;

-dupa unghiuri triedre;

-dupa distante intre muchiile opuse;

-dupa unghiuri formate de muchiile opuse;

-dupa lungimile sau poziţiile reciproce ale unor linii importante din tetraedru. Avand in ve­dere largile posibilitati de individualizare a unor tetraedre particulare, se impune fixarea atentiei doar asupra unor particularizari ce asigura suficiente proprietati geometrice supli­mentare.

§ 3, VOLUMUL TETRAEDRULUI

Definiţie: Volumul tetraedrului ABCD este produsul dintre aria unei fete si o treime din lungimea inaitimii perpendiculare pe ea.

Volumul tetraedrului ABCD se va nota prin VABCD sau |ABCD|; cand nu vor fi posibi­le confuzii se va nota doar V.

Urmatoarea lema asigura ca definiţia data este corecta.

Lema: Intr-un tetraedru, produsul dintre aria unei fete si inaltimea corespunzătoare nu depinde de alegerea fetei.

Demonstraţie:

fig.1

 

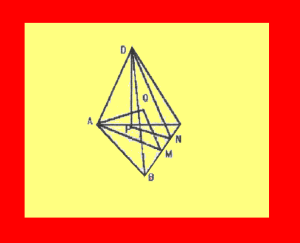
Fie |AM| , |DN| înălţimile triunghiurilor ABC si DBC. Fie |AQ| , |DP| inaltimi ale tetraedrului (fig.1). Conform teoremei celor trei perpendiculare QMA si DNP sunt unghiuri plane corespunzătoare unghiului diedru <A(BC)D = BC, deci sunt egale. In consecinţa, comple­mentele lor, QAM si PDN au aceeaşi masura, a=alfa . Urmeaza cos a = AQ / AM = PD / ND deci AQ • DN = AM • DP. Amplificând aceasta egalitate cu BC / 6 si tinand cont ca pentru ariile SA si SD ale fetelor [BCD] si [ABC] sunt valabile formulele SA = 1/2 • DN • BC, respectiv SD = 1/2 • AM • BC se obţine: 1/3 • SA • AQ = 1/3 • SD • DP.  Dar, intr-un tetraedru, oricare doua fete au o latura comuna, deci oricare ar fi fata aleasa cu inaltimea corespunzătoare, produsul ariei fetei cu lungimea inaitimii dusa pe ea este acelaşi.

Teorema 1 : (Proprietatea de aditivitate pentru volume). Fie un tetraedru ABCD si un plan prin dreapta AD care taie muchia BC intr-un punct interior M, atunci: VABCD = VDAMC + VDAMB .

Demonstraţie:

Se observa ca SABC = SAMC + SAMB. Inmulţind acesta egaliate cu 1/3 • DP, unde DP este lungimea inaltimii dusa din vârful D pe fata ABC, se obţine relaţia ceruta.

Consecinţa 1 : Daca M este un punct interior triunghiului ABC, atunci are ioc:

V ABCD = V ABMD  + V AMCD + VMBCD .

Intr-adevar, daca N €(AM) n (BC), conform teoremei 1 au loc:

VABCD= VANCD + VABND       VANCD = VAMCD +VMNCD

VABND=VABMD +VMBND si VMNCD +VMBND =VMBCD

Cu aceste egalitati urmeaza imediat formula din enunţ.

Consecinţa 2 : Daca M este un punct interior tetraedrului ABCD, atunci are loc:

VABCD= VMBCD +VMACD +VMABD +VABCM

Intr-adevar, dreapta DM, interioara triedrului D(unghiul triedru < D(ABC)) taie fata [ABC] intr-un punct interior M (teorema *)

Teorema * : Int. O(ABC) este locul geometric al punctelor M interioare unghiurilor AOX,unde X € Int (BOC).

Demonstraţie:

Un punct X interior unghiului BOC este interior diedrului B(OA)C. Urmeaza ca semiplanul (OA, X) este interior diedrului considerat. Un punct M din Int (AOX) se gaseste in interio­rul unghiurilor diedre A(OB)C si A(OC)B.

Reciproc, daca M este interior triedrului O(ABC), atunci semiplanul (OA,M) este interior diedrului B(OA)C si intersectează segmentul BC intr-un punct ce il putem nota cu X. Desigur, X € Int (BOC). Apoi semiplanul (OB,M), interior diedrului A(OB)X interceptează segmentul AX intr-un punct Y. OY este semidreapta interioara unghiului AOX, deci M € int (AOX).

Se aplica in mod convenabil consecinţa 1 pentru tetraedrele ABCD si ABCM. Consecinţa 3: Daca M este interior unghiului triedru D(ABC) fara a fi interior tetraedrului ABCD si nici situat pe fata ABC atunci are loc:

VABCD =VABMD +VMBCD+ VAMCD -VABCM •

Intr-adevar, deoarece M € Int D(ABC), exista N interior triunghiului ABC situat pe semi­dreapta (DM). Ipotezele mai asigura ca (ABC) separa punctele D si M, deci are loc D – N – M. Conform teoremei 1 au loc :

VABMD =VABMN +VABND , VMBCD= VMBCN+VNBCD si VAMCD = VAMCN + VANCD

Se aplica si consecinţa 2 tetraedrelor ABCD si ABCM avand punctul N interior unei fete.

§ 4. DREPTE CONCURENTE: METODE DE DEMONSTRARE A CONCURENTEI DREPTELOR

Problemele privind concurenta dreptelor pot fi separate in:

-probleme privind concurenta a doua drepte;

-probleme privind concurenta a trei sau mai multor drepte.

Rezolvarea problemelor privind concurenta a doua drepte in spaţiu poate cuprinde tehnici foarte variate, toate acestea incluse, prin ideea comuna in:

             Metoda I: Daca dreptele a si b sunt coplanare si nu sunt parafele, atunci ele sunt concurente.

In ceea ce priveşte demonstrarea coplanaritatii a doua drepte, cel mai adesea se utilizeaza tehnica: se identifica cate doua puncte distincte pe fiecare dreapta despre care se arata ca sunt coplanare; evident atunci dreptele sunt coplanare.

Pentru rezolvarea problemelor de tipul a) cat si de tipul b) dispunem de următoa­rea metoda cu caracter general.

            Metoda a ll-a : Fiind date dreptele d,, d2, …, dn intr-o „configuraţie” F de  puncte din spaţiu, se identifica in configuraţia F un punct special caruia ii sunt incidente toate dreptele d1, d2, …, dn.

           Metoda a lll-a : Daca trei plane a, ß, þ  au oricare doua cate un punct comun, atunci muchiile a cate doua din ele sunt concurente sau paralele intre ele.

Demonstraţie:

Prin ipoteza, planele ß, si þ au un punct comun si deci conform axiomei: Daca doua plane æ si ß  sunt incidente unui punct A, atunci exista inca (cel puţin) un punct B, diferit de A, incident fiecaruia din planele, æ si ß au o dreapta comuna, notata a; fie b,c analoagele lui a. Daca dreapta a intersectează planul æ  intr-un punct, sa-i zicem A, atunci punctul A este comun dreptelor a,b,c. In caz contrar (cand a este paralela cu planul æ  ), orice plan care trece prin a, deci atat ß  cat si þ  intersectează pe æ  dupa o paralela cu a, adica dreptele b,c sunt paralele cu a.

           Metoda a IV-a : Daca dreptele a,b,c nu sunt coplanare dar oricare doua sunt secante, atunci dreptele a,b,c sunt concurente.

Demonstraţie:

Dreptele b,c fiind secante, fie A punctul lor comun si æ  planul ce le include. Fie B € anc,C € anb. Daca punctele A, B, C ar fi distincte, dreapta a ar avea punctele distincte B si C incidente planului æ  , deci ar fi coplanara cu a si b, absurd. Daca B = A # C dreptele a si b ar fi confunde si nu secante. Analog conduce la absurd ipoteza ca  in {A,B,C} ar exista doua puncte distincte. Singura eventualitate ramasa A = B = C, exprima concurenta dreptelor a,b,c.